Quando
uma diferença de potencial ΔV é fornecida às extremidades de um fio condutor
que possui uma resistência igual a R, um campo elétrico é gerado que, por
sua vez, dá origem a uma corrente I dentro do material analisado. A parir dessa
análise, é possível concluir que quanto maior for a resistência, menor será a
corrente para a mesma tensão. Essa associação simples é conhecida
como lei de Ohm.
Entretanto, por mais simples que seja
essa associação, é necessário ter em mente que a resistência é uma
característica especifica de cada condutor. Isso se dá pelo fato de que ela
está ligada diretamente ao comprimento L, a área de seção transversal A e
a resistividade ρ do material do qual ele é constituído. Portanto,
utilizando a 1ª lei de Ohm, é possível deduzir que a resistência de um fio
condutor aumenta à medida que seu comprimento aumenta devido a uma maior
dificuldade em locomover os elétrons através de um fio longo do que através de
um fio mais curto. Além disso, conclui-se que ao diminuir a área da secção
transversal, se aumenta, também, a resistência, pois o mesmo campo elétrico
terá que empurrar mais elétrons em um fio largo do que em um fio fino. Com base
nessas análises, Georg Simon Ohm
conseguiu elaborar a expressão abaixo e a denominou de 2ª lei de Ohm.
Uma
informação importante que as vezes provoca duvidas é a compreensão de que a resistividade
e resistência não são a mesma coisa. Portanto, para que fique claro, temos que
a resistividade descreve apenas o material, e não, qualquer pedaço particular
do mesmo, enquanto a resistência caracteriza um pedaço especifico do condutor,
dotada de uma geometria especifica. Podemos estabelecer uma relação análoga
entre a resistividade e a resistência com a densidade e a massa para que o
entendimento seja mais pleno.
Para grande parte dos materiais a
resistividade irá variar conforme a mudança de temperatura do meio. Essa
mudança poderá ser calculada utilizando a seguinte equação:
Onde ρ é a resistividade à
temperatura final T e ρ༚ é a resistividade à
temperatura inicial T༚.
A constante α
é chamada de coeficiente de temperatura da resistividade e o seu valor pode ser
encontrado em uma tabela de confiança. Caso temperaturas bem mais baixas sejam
analisadas, efeitos novos podem ocorrer, tais como a supercondutividade, ou
seja, o desaparecimento brusco da resistência.
Outra
informação importante que vale ser ressaltada é o fato de que a lei de Ohm não
é uma lei da natureza. As afirmações desta lei são limitadas aos materiais cuja
a resistência se mantem constante ou aproximadamente constante quando
utilizados. Estes materiais são denominados de materiais ôhmicos, enquanto os
materiais que se comportam de tal modo que a corrente que o atravessará não
será diretamente proporcional a tensão aplicada, são chamados de materiais
não-ôhmicos.
As leis de Ohm terão um impacto direto no desenvolvimento do nosso projeto, uma
vez que o cálculo da resistência é essencial para encontrar as diversas outras
variáveis. Por exemplo, a partir da tabela AWG, verificamos que o fio utilizado
possui uma capacidade máxima de corrente, ou seja, caso passe mais corrente do
que o estabelecido, o fio irá fundir. Além disso, existe a possibilidade do
esmalte que o reveste derreta, causando um contanto entre os fios e,
consequentemente, um curto-circuito.
Após
dimensionar o tamanho do fio para que a corrente não ultrapasse o limite,
obteremos o número de espiras, a potência dissipada, o valor do campo magnético
e o fluxo magnético. Com o cálculo da variação do fluxo magnético em função do
tempo, obteremos a forca eletromotriz induzida no anel, ou seja, aplicando a 2ª lei de Ohm, encontraremos a resistência elétrica do anel e, logo em seguida,
aplicando a 1ª lei de Ohm, obteremos a corrente induzida no mesmo. Com o valor
da corrente induzida, podemos calcular a forca magnética que irá provocar o
movimento do anel.
Referências:
NUSSENZVEIG, H. M. Curso de física
básica: Eletromagnetismo. 1ª Edição. São Paulo: Blucher, 1997. v.3.
SADIKU, M. N. O. Elementos de eletromagnetismo.
5ª Edição. Porto
Alegre: Bookman, 2012. 704 p.
KNIGHT, R. D. Física: Uma
abordagem estratégica. 2ª Edição. Porto Alegre: Bookman, 2009. v.3.
HALLIDAY, D. Fundamentos de física:
Eletromagnetismo. 9ª Edição.
Rio de Janeiro: LTC, 2012. v.3.
Publicado por: Bruno Corrêa Arvan
Publicado por: Bruno Corrêa Arvan
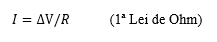


Nenhum comentário:
Postar um comentário